Markov Zinciri Programlamaya Giriş

Varsayalım ki yarın havanın güneşli mi yoksa yağmurlu mu olacağını bilmek istiyoruz. Deneyimlerinize ve hava durumu hakkındaki tarihsel gözleminize dayanan doğal bir sezgimiz olabilir. Son 1 hafta boyunca hava güneşliyse, yarının da güneşli olacağına dair %90 yağar şeklinde bir öngörümüz olabilir. Ancak bir önceki hafta ya da  başka bir zamana hava yağmurlu olsaydı, yarının güneşli olma ihtimali pek olası gözükmez sadece% 50 şansı olurdu. Bu senaryo Markov Zinciri işlemi olarak tanımlanabilir.

Markov Zinciri nedir?

Ama resmi olarak Markov Zinciri nedir? Markov Zinciri, belirli stokastik veya olasılık kurallarına göre bir durumdan diğerine geçişlerin bir koleksiyonunu tanımlayan matematiksel bir sistemdir.
Örneğin, sonraki günün hava durumunu tahmin etmek için önceki senaryomuzu ele alalım. Bugün hava güneşliyse, deneyimimize göre, yarın havanın yağmurlu duruma geçme olasılığı %10 ve güneşli % 90’dır. Öte yandan, şu anda hava yağmurluysa, yarın yağmurlu kalma olasılığı % 50 ve güneşli olması % 50’dir.

Farklı durumlar arasındaki bu değişiklikler (veya bunların eksikliği) geçişler olarak adlandırılırken ilgi değişkeni (yani. yağmurlu veya güneşli) durumlar olarak adlandırılır.

Ancak bu geçişlerin Markov Zinciri olarak nitelendirilebilmesi için Markov Mülkiyetini tatmin etmeleri gerekmektedir. Bu özellik, geçiş olasılığının, önceki diziler kümesine değil, yalnızca mevcut duruma bağlı olduğunu belirtir. Bu özellik Markov Zincirinin hafızasız olmasını sağlar.

Neden Markov Zinciri?

Şimdi Markov Zincirinin ne olduğunu ele aldığımıza göre, aşina olmanın neden değerli olduğunu tartışalım. Markov Zinciri, oyun teorisi, fizik, ekonomi, sinyal işleme, bilgi teorisi ve daha birçok gibi gerçek dünyadaki süreçlerde birçok uygulamaya sahiptir.

Ayrıca, bu görünüşte basit süreç, Markov Zinciri Monte Carlo (MCMC) veya Gizli Markov Zinciri gibi daha karmaşık stokastik simülasyon yöntemlerinin temelini oluşturur. Ayrıca Markov Chain, Bayesian istatistiklerinin yapı taşlarından biri olmak gibi modern veri bilimi tekniklerinin çoğunun öncüsüdür.

Markov Zinciri, veri bilimindeki daha gelişmiş istatistiksel modelleme tekniklerini anlamanız için iyi bir başlangıç noktası olarak hizmet edecektir. Bu nedenle, Markov Sürecinin temellerini matematiksel bir anlayış ile anlayarak ve algoritma uygulamasını kodlayarak ellerimizi kirletmek kaçınılmazdır.

Markov Zinciri Hakkında Daha Fazla Bilgi: Matematiksel Tanım

Markov Zinciri modeli, geçiş matrisi olarak durum geçişlerinin olasılıklarını temsil eder. Sistemin adet N olası durumları varsa (örn. Hava tahmini durumumuz için N=2), daha sonra geçiş matrisi N x N şeklinde bir geçiş matrisine sahip olacaktır. Daha sonra, matris için bireysel giriş, N (i, j), durum i ve durum j arasındaki geçiş olasılığını gösterecektir.

Markov Zinciri Programlama

Yukarıdaki örneği Python’da kodlamayı deneyelim.

1. Gerekli kütüphaneleri yükleyelim

import numpy as np
import random as rm

2. Durumları ve olasılıklarını tanımlayalım (NOT: her satırdaki toplam olasılığın 1’e kadar çıkmasını sağlamamız gerek)

states = ["sunny", rainy"]
transitions = [["SS", "SR"],["RS", "RR"]]
T = [[0.9, 0.1],[0.5, 0.5]] #possibility

3. Önümüzdeki n sayıda gün için hava durumunu tahmin etmek için  Markov Zinciri fonksiyonunu yazalım

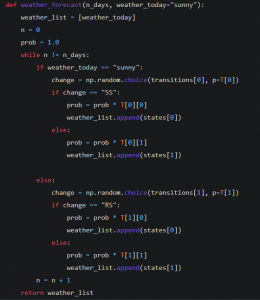
Programı önümüzdeki 5 gün için çalıştıralım.

future_weathers = weather_forecast(n_days = 5)

Sonuç

Markov Zinciri’nin tanımlayıcı ve resmi olarak ne olduğunu ve temel ilkesini öğrenmenin neden önemli olduğunu ele aldık. Ayrıca çok temel bir Markov sürecini sıfırdan kodladık. Artık bir Markov Zincirinin nasıl çalıştığını bildiğimize göre, Gizli Markov Süreci veya MCMC gibi daha karmaşık stokastik modelleme tekniklerine derinlemesine dalabiliriz.