
Bu makalede, zaman serilerinin dünyasını ve python kullanarak mevsimsel verileri tahmin etmek için SARIMA modelinin nasıl uygulanacağını keşfedeceğiz.
Neden Doğal Gaz Depolama Verileri?
Haftalık doğal gaz depolama verileri, halkın doğal gaz envanter seviyelerini, doğal gaz piyasasındaki arz ve talep dengesinin göstergelerini belirlemek için kullandığı temel bir federal ekonomik göstergedir. ABD Enerji Bilgi İdaresi’ne göre, raporun yayınlanması üzerine, doğal gaz piyasası, önceki haftadan itibaren doğal gaz fiyatlarını etkileyen envanter seviyelerinde elde edilen net değişime tepki veriyor.
Proje Ön Koşulları
Bu projeyi yürütmek için numpy, pandas, matplotlib, sklearn ve statsmodels kitaplıklarını kullanacağız. Yerel sisteminize henüz yüklemediyseniz, aşağıdaki kodu komut isteminde kullanabilirsiniz:
pip install numpy
pip install pandas
pip install matplotlib
pip install -U scikit-learn
pip install statsmodels
Veri ve Kütüphaneleri İçe Aktarma
Python’da numpy, pandas, matplotlib, sklearn ve istatistik modelleri gibi işimizi kolaylaştıracak çeşitli kütüphaneleri içe aktararak modeli oluşturmaya başlayalım.
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_log_error
%matplotlib inline
Ardından, bu analizde kullanılan veri setine ABD ÇED’in web sitesinden (Haftalık Doğal Gaz Depolama Raporu) erişmeye çalışalım. Çıktıda, veri sayfasının son beş öğesini görebilirsiniz.
#Import data from EIA – Weekly Natural Gas Storage Report
data = pd.read_csv(‘NaturalGasStorageUS.csv’)
data.tail()

Veri Setini Görselleştirme
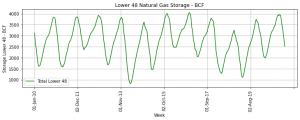
2010 ile 2021 arasındaki hafta sonu ile toplam alt 48 gaz depolama sütunu arasındaki grafiği çizelim. Bu görselleştirmenin kodunu aşağıda görebilirsiniz:
#Visualize the total natural gas storage data since 2010
plt.figure(figsize=[12, 5]); # Set dimensions for figure
data.plot(x=’Week ending’, y=’Total Lower 48′, figsize = (12, 3.5), legend = True, color=’g’)
plt.title(‘Lower 48 Natural Gas Storage – BCF’)
plt.ylabel(‘Storage Lower 48 – BCF’)
plt.xlabel(‘Week’)
plt.xticks(rotation=90)
plt.grid(True)
plt.show()
Veri Setinin Durağanlığını Test Etme
Zaman serilerinin sabit olup olmadığını belirlemeye yardımcı olabilecek iyi bilinen istatistiksel bir test olan Augmented Dickey-Fuller Testini kullanalım. ADF testi, bir tür birim kök testidir. Birim kökleri durağan olmamanın bir nedenidir, ADF testi birim kökün olup olmadığını test eder. Sıfır Hipotezi, bir birim kökün varlığını belirtir. P-Değeri tanımlanan Önem Seviyesinden düşükse, zaman serilerinin bir birim kök içerdiğine dair Sıfır Hipotezini reddederiz. Başka bir deyişle, Sıfır hipotezini reddederek, zaman serilerinin durağan olduğu sonucuna varabiliriz.
# Augmented Dickey-Fuller test ad_fuller_result = adfuller(data['Total Lower 48']) print(f'ADF Statistic: {ad_fuller_result[0]}') print(f'p-value: {ad_fuller_result[1]}')ADF Statistic: -5.520456690936758 p-value: 1.8827985107022387e-06
Burada p değeri 0,05’ten küçüktür ve sıfır hipotezini reddedebiliriz, yani zaman serisi durağandır.
SARIMA Modelini Oluşturalım
Zaman serimizin durağan olduğunu belirledikten sonra, gelecekteki değerleri tahmin etmek için SARIMA modelini kullanabiliriz. Modelin gösterimi SARIMA’dır (p, d, q). Bu üç parametre, verilerdeki mevsimsellik, eğilim ve gürültüyü hesaba katar. Belirli bir veri kümesi için istatistiksel modellerin göreceli kalitesinin bir tahmin edicisi olan AIC’yi (Akaike bilgi kriteri) hesaplamaya çalışalım. Veriler için bir model koleksiyonu verildiğinde, AIC her modelin kalitesini diğer modellerin her birine göre tahmin eder. Düşük AIC değeri model için daha iyidir. Çıktı, 5445 AIC değerine sahip SARIMAX (2, 1, 1) x (2, 1, 1, 52) ‘nin en iyi kombinasyon olduğunu öne sürüyor, bu nedenle bunu en uygun seçenek olduğunu düşünüp modele devam ediyoruz.
best_model = SARIMAX(data['Total Lower 48'], order=(2, 1, 1), seasonal_order=(2, 1, 1, 52)).fit(dis=-1) print(best_model.summary())SARIMAX Results ========================================================================================== Dep. Variable: Total Lower 48 No. Observations: 580 Model: SARIMAX(2, 1, 1)x(2, 1, 1, 52) Log Likelihood -2715.678 Date: Sun, 14 Feb 2021 AIC 5445.356 Time: 09:27:48 BIC 5475.226 Sample: 0 HQIC 5457.050 - 580 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 1.0854 0.236 4.596 0.000 0.623 1.548 ar.L2 -0.2184 0.107 -2.036 0.042 -0.429 -0.008 ma.L1 -0.7386 0.227 -3.260 0.001 -1.183 -0.295 ar.S.L52 -0.0678 0.055 -1.234 0.217 -0.176 0.040 ar.S.L104 -0.1674 0.047 -3.581 0.000 -0.259 -0.076 ma.S.L52 -0.8039 0.067 -12.064 0.000 -0.934 -0.673 sigma2 1525.3882 67.365 22.644 0.000 1393.356 1657.421 =================================================================================== Ljung-Box (Q): 29.95 Jarque-Bera (JB): 172.85 Prob(Q): 0.88 Prob(JB): 0.00 Heteroskedasticity (H): 1.21 Skew: -0.39 Prob(H) (two-sided): 0.21 Kurtosis: 5.70 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).
Modeli verilere göre ayarladıktan sonra, model uyumunun geçerliliğini doğrulamak için kalan grafikleri kontrol ederiz.
#Diagnosing the model residuals
best_model.plot_diagnostics(figsize=(15,12));
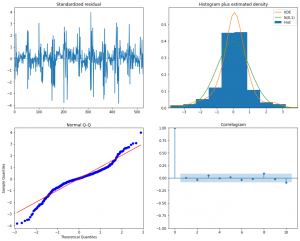
Normal Q-Q grafiğinden, neredeyse düz bir çizgiye sahip olduğumuz çıkarılabilir, bu da normallikten sistematik bir ayrılmanın olmadığını gösterir.
Tahmin
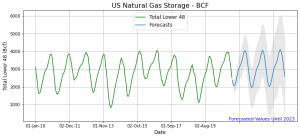
Tahmin adımında, önümüzdeki 156 adım veya 3 yıl için Toplam Alt 48 doğal gaz depolama verisini tahmin etmeye çalışacağız. Aşağıdaki grafik, geçmiş depolama verilerine dikkate değer bir uyumu göstermektedir.
#Forecasting 3 years steps ahead
forecast_values = best_model.get_forecast(steps = 156)
#Confidence intervals of the forecasted values
forecast_ci = forecast_values.conf_int()
#Plot the data
ax = data.plot(x=’Week ending’, y=’Total Lower 48′, figsize = (12, 5), legend = True, color=’g’)
#Plot the forecasted values
forecast_values.predicted_mean.plot(ax=ax, label=’Forecasts’, figsize = (12, 5), grid=True)
#Plot the confidence intervals
ax.fill_between(forecast_ci.index,
forecast_ci.iloc[: , 0],
forecast_ci.iloc[: , 1], color=’#D3D3D3′, alpha = .5)
plt.title(‘US Natural Gas Storage – BCF’, size = 16)
plt.ylabel(‘Total Lower 48 (Bcf)’, size=12)
plt.xlabel(‘Date’, size=12)
plt.legend(loc=’upper center’, prop={‘size’: 12})
#annotation
ax.text(570, 100, ‘Forecasted Values Until 2023′, fontsize=11, color=’blue’)
plt.show()
Tahmini Doğrulama
Model performansını değerlendirmek için, modelin gerçekliğini test etmek için R-kare puanını ve veri setinin hata ortalamasının karekökünü hesaplıyoruz.
R Kare aynı zamanda ayrıca belirleme katsayısı olarak da bilinir. Bu metrik, bir modelin belirli bir veri kümesine ne kadar iyi uyduğunun bir göstergesidir. Regresyon çizgisinin (yani çizilen tahmin edilen değerler) gerçek veri değerlerine ne kadar yakın olduğunu gösterir. R kare değeri, 0 ile 1 arasındadır; burada 0, bu modelin verilen verilere uymadığını ve 1, modelin sağlanan veri kümesine mükemmel şekilde uyduğunu gösterir. Modelin% 99,7 doğruluğu var ve bu değer oldukça iyi.
Kök Ortalama Kare Hata (RMSE), dikey bir çizgi boyunca ölçülen, takılan çizgiden ortalama olarak bir veri noktasının mesafesidir. 30.3 olan RMSE değeri, ölçüm birimleri açısından doğrudan yorumlanabilir ve modelin gelecekte doğru tahmin etme becerisine güvenmemiz için yeterince düşüktür.
#divide into train and validation set to calculate R-squared score and mean absolute percentage error
train = data[:int(0.85*(len(data)))]
test = data[int(0.85*(len(data))):]
start=len(train)
end=len(train)+len(test)-1
predictions = best_model.predict(start=start, end=end, dynamic=False, typ=’levels’).rename(‘SARIMA Predictions’)
evaluation_results = pd.DataFrame({‘r2_score’: r2_score(test[‘Total Lower 48’], predictions)}, index=[0])
evaluation_results[‘mean_absolute_error’] = mean_absolute_error(test[‘Total Lower 48’], predictions)
evaluation_results[‘mean_squared_error’] = mean_squared_error(test[‘Total Lower 48’], predictions)
evaluation_results[‘root_mean_squared_error’] = np.sqrt(mean_squared_error(test[‘Total Lower 48’], predictions))
evaluation_results[‘mean_absolute_percentage_error’] = np.mean(np.abs(predictions – test[‘Total Lower 48’])
/np.abs(test[‘Total Lower 48’]))*100
evaluation_results
![]()
Sonuç
Genel olarak, 2025 yılına kadar doğal gaz depolama sayılarını öngören SARIMA modelimizin kalitesi oldukça yüksektir.
Python’da zaman serilerini nasıl modelleyebileceğimizi, gelecekteki değerleri nasıl tahmin edebileceğimizi ve modeli doğrulayabileceğimizi anlamak için zaman ayırdığınız için teşekkür ederiz.
